Seminar index
25th Hakubi Seminar
Infinity in Mathematics
- Speaker:Nobu KISHIMOTO(The Hakubi Center)
- Date:6th September 2011 (Tuesday), 16:00-
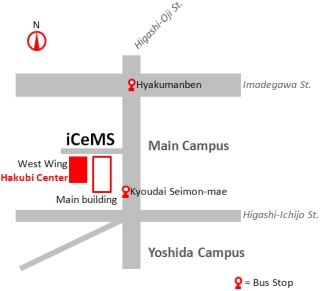
- Venue:The Hakubi Center (iCeMS West Wing 2F, Seminar Room)
- Presentation Language:English
Summary
We often describe a very great number as “infinity,” even though it does not necessarily mean “not finite.” For instance, even an “infinite” number of twinkling stars actually exist in finite amounts (to our knowledge, at least). Meanwhile, the infinity of mathematics really means “not finite.” For instance, natural numbers (positive numbers with no fractional portion, i.e. {1, 2, 3, …}) really do exist infinitely, and we can find many more natural numbers than the total number of stars. Due to the finiteness of our time, it is impossible to count all natural numbers one by one. We understand them through a thought experiment of infinite-time counting. How, then, can we comprehend all numbers, including fractions and decimals? We cannot count them in a regular manner, since they exist densely and not in a row. In mathematics, we often represent some object as a result of infinite repetition of some operation. However, it is controversial to say which kind of operations can be infinitely repeated to create an object with some meaning. Even the “number” itself, the most fundamental object in mathematics, requires quite abstruse procedures in order to be defined rigorously. In this seminar, I will try to give a basic explanation of the mathematical approach toward these issues. If time allows, I will discuss some topics related to my research field, differential equations.